Theory + Abstractions¶

Mathematical background¶

The mathematical formulation used by ChiDG considers first a partial differential equation in conservation form

\[\frac{\partial Q}{\partial t} + \nabla \cdot \vec{F}(Q,\nabla Q) + S(Q,\nabla Q) = 0\]

The solution(\(Q\)) is expressed as an expansion in basis polynomials constructed as a tensor product of 1D Legendre polynomials as

\[Q(t,x,y,z) = \sum_{i=0}^N \sum_{j=0}^N \sum_{k=0}^N Q_{ijk}(t) \psi_i(x) \psi_j(y) \psi_k(z)\]

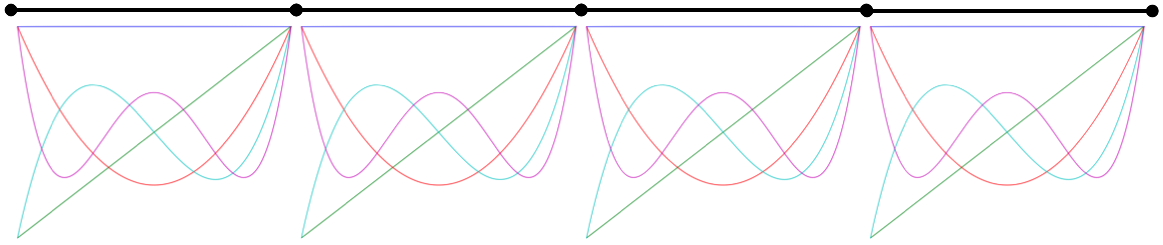
A representation of the discontinuous Galerkin method for 1D elements showing, in each element, a polynomial expansion that represents the solution in that element.

Multiplying by a column of test functions \(\boldsymbol{\psi}\) and applying Gauss’ Divergence Theorem gives our working form of the discontinuous Galerkin method as

\[\int_{\Omega_e} \boldsymbol{\psi} \frac{\partial Q}{\partial t} d\Omega + \int_{\Gamma_e} \boldsymbol{\psi} \vec{F} \cdot \vec{n} d\Gamma - \int_{\Omega_e} \nabla \boldsymbol{\psi} \cdot \vec{F} d\Omega + \int_{\Omega_e} \boldsymbol{\psi} S d\Omega = 0\]

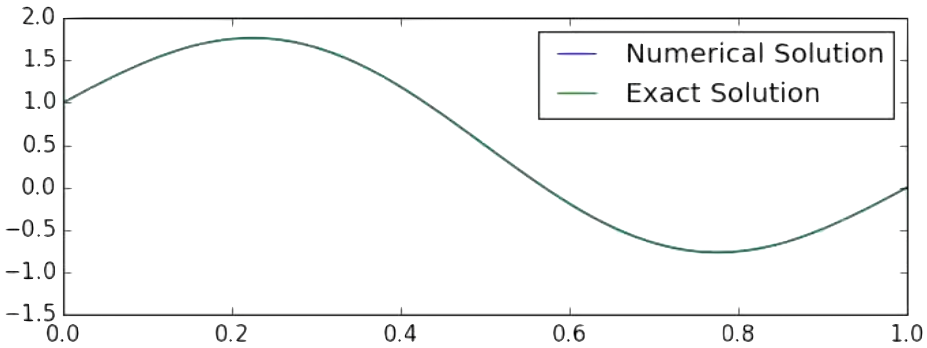
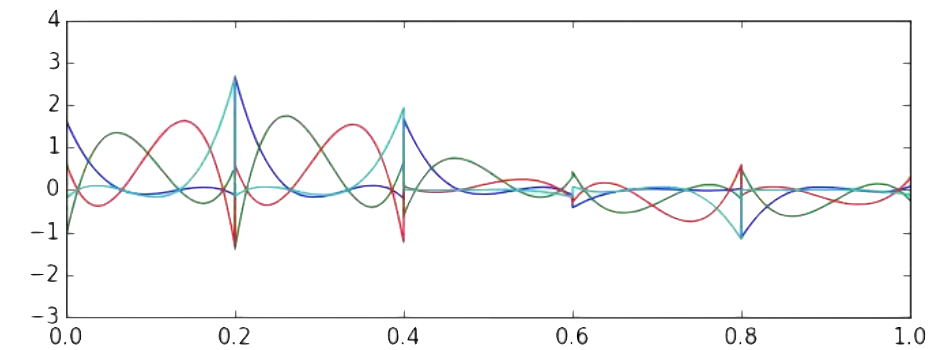
A 1D DG Solution of a linear poisson equation

Reconstructed solution

Polynomial modes that produce the solution

There are three spatial integral operators in the equation above. These are the Boundary Integral, Volume Integral, and Source term Integral:

Boundary Flux Integral	\[\int_{\Gamma_e} \boldsymbol{\psi} \vec{F} \cdot \vec{n} d\Gamma\]
Volume Flux Integral	\[\int_{\Omega_e} \nabla \boldsymbol{\psi} \cdot \vec{F} d\Omega\]
Volume Source Integral	\[\int_{\Omega_e} \boldsymbol{\psi} S d\Omega\]

In order to solve a set of equations in the discontinuous Galerkin framework, these integral functions must be implemented for the specific equation set being solved. It might not be, that each integral operator needs to be implemented, just the ones that represent the equation set being solved. So, for example, the Euler equations for nonlinear compressible flows do not have a source term, so there is no need to implement a volume source integral. In general, for conservation laws of the form

\[\nabla \cdot F(Q) = 0\]

a Boundary Flux Integral and Volume Flux Integral will need to be implemented for the term \(F(Q)\). ChiDG represents each implemented integral operator as its own object, operator_t.

ChiDG Operators¶

The integral expressions in the discontinuous Galerkin formulation are represented in ChiDG as operator_t objects. Each new integral term that one wishes to implement is extended from the operator_t base class. These objects do not contain much data. Rather, they primarily hold a type-bound procedure compute that allows the function definition to be passed around, stored as an array of operator_t‘s, etc.

type, abstract :: operator_t

contains

    procedure, deferred   :: init
    procedure, deferred   :: compute

end type operator_t

When a new operator is defined, it is required that the class type-bound procedures init and compute also be implemented. These are not implemented for the abstract base class because they do not have any meaning until they are associated with a specific implementation.

init(self)¶

The operator initializaton routine requires several bits of information to be implemented when defining a new operator.

#1 Set the name of the operator

Example

call self%set_name("Roe Flux")

#2 Set the equations that the operator will be operating on:

Example

call self%set_equation("Pressure")

Example

call self%set_equation("Density")

call self%set_equation("X-Momentum")

call self%set_equation("Energy")

compute(worker, prop)¶

Implement the function that is operating on the data. Compute the function values, and call an integration routine.

Parameters:	worker (chidg_worker_t) – A chidg_worker_t instance that acts as an interface for providing data, integrating, etc. prop (properties_t) – A properties_t instance

Registering new operators¶

Any time a new operator_t is defined, in order for it to be used, it must be registered in the operator factory. This is located in mod_operators.f90. This informs the framework that the operator exists, and allows the operator to be used by equation sets through the operator factory.

Note

Register new operators inside mod_operators.f90

#1: Import the operator definition

use type_new_operator.f90, only: new_operator_t

#2: In the module procedure register_operators, create an instance of the operator and add it to the operator factory

type(new_operator_t) :: my_new_operator

call operator_factory%register(my_new_operator)

Note: register_operators gets called on startup so any operators defined and registered there are created and added to the framework at startup.

ChiDG Equation Sets¶

ChiDG takes a composition approach to defining sets of equations, and this is represented in an equation_set_t object. equation_set_t‘s contain arrays of operator_t instances. In this way, operator_t‘s can be added to equation sets to represent additional equations or additional terms that represent another phenomenon.

class equation_set_t¶

type :: equation_set_t
    type(operator_t)    volume_advective_operator(:)
    type(operator_t)    boundary_advective_operators(:)
    type(operator_t)    volume_diffusive_operator(:)
    type(operator_t)    boundary_diffusive_operators(:)
    ...
contains

    procedure, public :: add_operator

end type equation_set_t

add_operator(string)¶

Accepts a string indicating an operator to add. Internally, the string is used to create the operator from a factory.

Parameters:	string (str) – The name of an operator to be added.

Tip

An equation_set_t that represents the Euler equations for nonlinear compressible flows might be composed of the following operator_t‘s:

Boundary Flux Operators	Euler Boundary Average Flux Roe Upwind Flux
Volume Flux Operators	Euler Volume Flux

Such an equation_set_t could be constructed using the following procedure:

#1: Create an instance of an equation_set_t:

type(equation_set_t) :: euler_equations

#2: Add operators to the new equation set:

call euler_equations%add_operator("Euler Boundary Average Flux")

call euler_equations%add_operator("Roe Upwind Flux")

call euler_equations%add_operator("Euler Volume Flux")

Note: The operators being added should already be implemented as extensions of operator_t and be registered in mod_operator.f90.